The first speaker was Mark Horley (@mhorley), who I have followed on twitter for a while. The focus of his talk was around supporting all students in mixed attainment classes, especially in KS3. At the school I work out, students are not set in year 7 so this was really interesting to me.
Mark talked mastery and really spending time with the pupils on ensuring they have truly grasped the concepts before rushing on. He used the examples of fractions, speaking about how he may do a whole lesson, just on adding fractions with the same denominator. He showed us a worksheet, which used scaffolding to assist students with adding fractions, but as the questions went on, the scaffolding was slowly removed, in a subtle way that meant students with low confidence didn't feel like they went from total support to no support.
Some examples of the questions were as follows:
This is definitely something I will explore with my new year 7 groups, giving this to some of my weaker students and the same questions, with less scaffolding, to my stronger students.
Mark then went on to talk about algebra and the importance of introducing in early in year 7. One thing that really interested me was the idea of discussing the distributive and associative laws in relation to algebra as well as number. This is something I would probably have done but unintentionally but it will be something I will be more explicit about when teaching algebra as I haven't had much of chance to teach algebra before. We had some interesting discussions surrounding these questions below and others we may use when looking at what information we can get from an equation.
Here are some of the questions:
1) when you multiply by 10, you add a zero
2) 3.4 x 100 = 3.400
3) 4.56 / 100 = 0.456
4) 340 / 10 = 34.0
5) 0.83 x 1000 = 83
6) Dividing by 100 is the same as dividing by 10 twice
7) To multiply by 100, you move the decimal place 2 places to the right
These are some wonderful questions to stimulate discussion and check deep understanding.
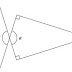
One thing I have used before but not really thought too deeply about is those maths problems in spider diagrams (no idea if there is an official name) where you have a number in the centre and operations to perform around it, like the image below.
These allow students to pick where they begin, which can help encourage students who dislike the structure and control of a worksheet by giving them some choice. Some students may under or overestimate the starting point they should take so some prompting of "You might like to start with this one..." if they are really struggling or don't like the freedom that comes with choice. Students that finish early could then be extended to add their own arrows which is a nice easy way to stretch those.
Another nice quick idea Mark mentioned was for filling in the boxes (which is a good follow on from primary) where you use a circle for operations and a box for numbers so it is clear if you have an operation and a number to fill in, which is needed.
We then went on the look at an activity called quarter the cross which I had seen before on Mark's website. Students would then need to shade in a quarter of the cross. What I had not thought about was getting the students to write a number sentence showing that what they have shaded is a quarter. Mark then showed us a complicated way of shading the cross (there are over 50 ways!) and we then had to try and write the number sentence to show it was a quarter. This activity could really be stretched but still accessible to those who struggle.
This post has now got too long because there was so much great information to take away so I will be another post on the other speakers at the conference. Thanks to Mark for such a wonderful and informative talk. I also sat on a table with Mark for the rest of the sessions and he was such a lovely guy!







No comments:
Post a Comment